Force Law for Simple Harmonic Motion

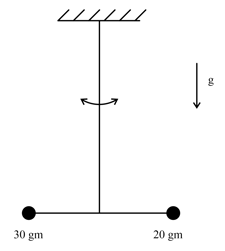
Two point-like objects of masses $20 \mathrm{gm}$ and $30 \mathrm{gm}$ are fixed at the two ends of a rigid massless rod of length $10 \mathrm{cm}$. This system is suspended vertically from a rigid ceiling using a thin wire attached to its center of mass, as shown in the figure. The resulting torsional pendulum undergoes small oscillations. The torsional constant of the wire is $1.2\times {10}^{-8} \mathrm{N} \mathrm{m} {\mathrm{rad}}^{-1}$. The angular frequency of the oscillations in $n\times {10}^{-3} \mathrm{rad} {\mathrm{s}}^{-1}$. The value of $n$ is _____.

In a linear Simple Harmonic Motion (SHM)

(A) Restoring force is directly proportional to the displacement.

(B) The acceleration and displacement are opposite in direction.

(C) The velocity is maximum at mean position.

(D) The acceleration is minimum at extreme points.

Choose the correct answer from the options given below:

A  $2 \mathrm{kg}$ block hangs without vibrating at the bottom end of a spring with a force constant of $400 \mathrm{N} {\mathrm{m}}^{-1}$. The top end of the spring is attached to the ceiling of an elevator car. The car is rising with an upward acceleration of $5 \mathrm{m} {\mathrm{s}}^{-1}$ when the acceleration suddenly ceases at time $t=0$ and the car moves upward with constant speed. $(g=10 \mathrm{m} {\mathrm{s}}^{-2}$)
What is the angular frequency of oscillation of the block after the acceleration ceases?
$$\begin{gathered} \mathrm{A}) 10\sqrt{2} \mathrm{rad} {\mathrm{s}}^{-1} \\ \mathrm{B}) 20 \mathrm{rad} {\mathrm{s}}^{-1} \\ \mathrm{C}) 20\sqrt{2} \mathrm{rad} {\mathrm{s}}^{-1} \\ \mathrm{D}) 32 \mathrm{rad} {\mathrm{s}}^{-1} \end{gathered}$$
The amplitude of the oscillations is 

$$\begin{gathered} \mathrm{A}) 7.5 \mathrm{cm} \\ \mathrm{B}) 5 \mathrm{cm} \\ \mathrm{C}) 2.5 \mathrm{cm} \\ \mathrm{D}) 1 \mathrm{cm} \end{gathered}$$

An ideal massless spring S can be compressed $2$metre by a force of$200 \mathrm{N}$. This spring is placed at the bottom of a frictionless inclined plane with makes an angle$\theta =30°$ with the horizontal. A $20 \mathrm{kg}$ mass is released from rest at the of the inclined plane and is brought to rest momentarily after compressing the spring 4 metre. Through what distance does the mass slide before coming to rest.$(g=10 \mathrm{m} {\mathrm{s}}^{-2})$
 

Two springs have respective force contain $k_1$ and $k_2$. Both are stretched till their elastic potential energies are equal.  If the stretching force are $f_1$ and $f_2$, find $\frac{f_1}{f_2}$.

A force of $10 \mathrm{N}$holds an ideal spring with a $20 \mathrm{N}/\mathrm{m}$ spring constant in compression. The potential energy stored in the spring is
 

What is meant by second pendulum?

Two magnets with the same dimensions and mass, but of magnetic moments ${\mu }_1=100 \mathrm{A} {\mathrm{m}}^2$ and ${\mu }_2=50 \mathrm{A} {\mathrm{m}}^2$  are jointly suspended in the earth's magnetic field. So as to perform angular oscillations in a horizontal plane. When their like poles are joined together the period of their angular S.H.M is $5 \mathrm{s}$. Find the period of angular S.H.M, when their unlike poles are joined together.

A long uniform rod of length $l$ and mass $\mathrm{m}$ is free to rotate in a horizontal plane about a vertical axis through its center. A spring of spring constant $k$ is connected horizontally between the end of the rod and a fixed wall as shown. What is the period of the small oscillations that result when the rod is pushed slightly to one side and released?

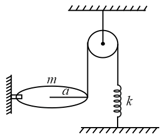
A ring is connected to an inextensible string which passes over a frictionless pulley. The other end of the string is connected to the upper end of a massless spring of spring constant $k$. The lower end of the spring is fixed. The ring of mass $m$ and radius $a$ can oscillate in the vertical plane about the hinge without any friction. If the horizontal position of the ring is in the equilibrium position, then the time period of the small oscillations of the ring is

A particle performs $SHM$ under the action of a force $F_1$ With frequency $3 \mathrm{Hz}.$ If force is changed to $F_2$ frequency of oscillation changes to $4 \mathrm{Hz}.$ If both forces act simultaneously in the same direction on the particle then find new frequency of oscillation (in $\mathrm{Hz}).$

A uniform rod of length $2l$ rocks to and fro on the top of a rough semicircular cylinder of radius a. The period of small oscillations is $T$. The value of $T\frac{\sqrt{3ga}}{l}$ is :

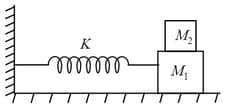
A block of mass $M_1$ resting on a frictionless horizontal surface connected to a spring of spring constant $k$ that is anchored to a wall. A block of mass $M_2=\alpha M_1$ is placed on the top of the first block. The two bodies move as a unit with S.H.M. What is the maximum amplitude of oscillation so that the two bodies move a unit? The coefficient of friction between two bodies is $\mu$.where $\alpha$ is a constant.

What Causes Periodic Motion?

Assertion : A particle is moving along $x-$axis. The resultant force $F$ acting on it is given by, $F=-ax-b$, where $a$ and $b$ are both positive constants. The motion of this particle is not SHM.

Reason : In SHM resultant force must be inversely proportional to the displacement from mean position.

The restoring force of SHM is maximum when particle

A rectangular pipe having cross-sectional area $A$. It is closed at one end and at its other end, a block having the same cross-section and mass $m$ is placed such that the system is airtight. In the equilibrium position of the block, the pressure and volume of air enclosed in the pipe are $P$ and $V$ respectively. If the block is displaced by a small distance $x$ inward and released then find the time period of S.H.M. [Assume the walls are frictionless and compression of air is isothermal].

Which of the following cannot be in the same direction for a simple harmonic oscillation?

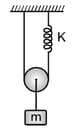
A mass $\mathrm{m}$ is suspended from a massless pulley, which it self is suspended by a massless string and a spring as shown in figure. The force constant of spring is $\mathrm{K}$ . What will be the time period of oscillation of $\mathrm{m}$: 

A particle is moving on $X$-axis and has potential energy $U=\left(2-20x+5x^2\right) \mathrm{J}$, where $x$ is position(in $\mathrm{m}$). The particle is released at $x=-3 \mathrm{m}$. If the mass of the particle is $0.1 \mathrm{kg}$, then the maximum velocity (in $\mathrm{m} {\mathrm{s}}^{-1}$) of the particle is $25\beta$ if amplitude is $5 \mathrm{m}$, then the value of $\beta$